|
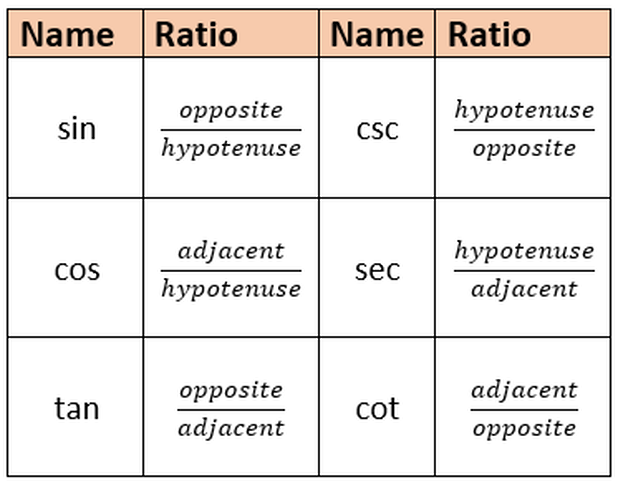
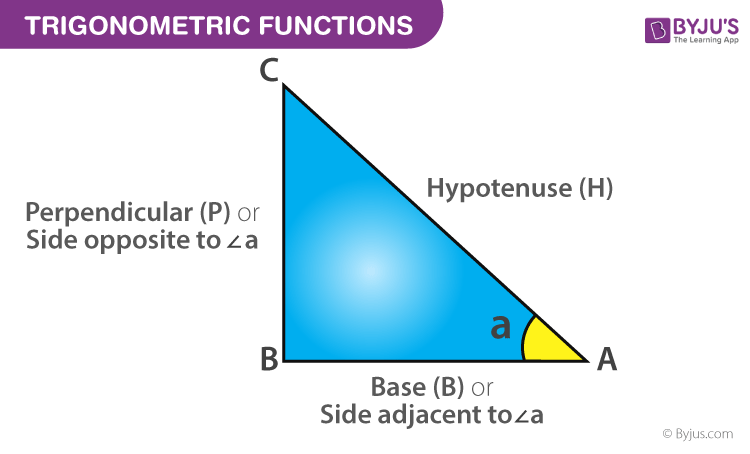
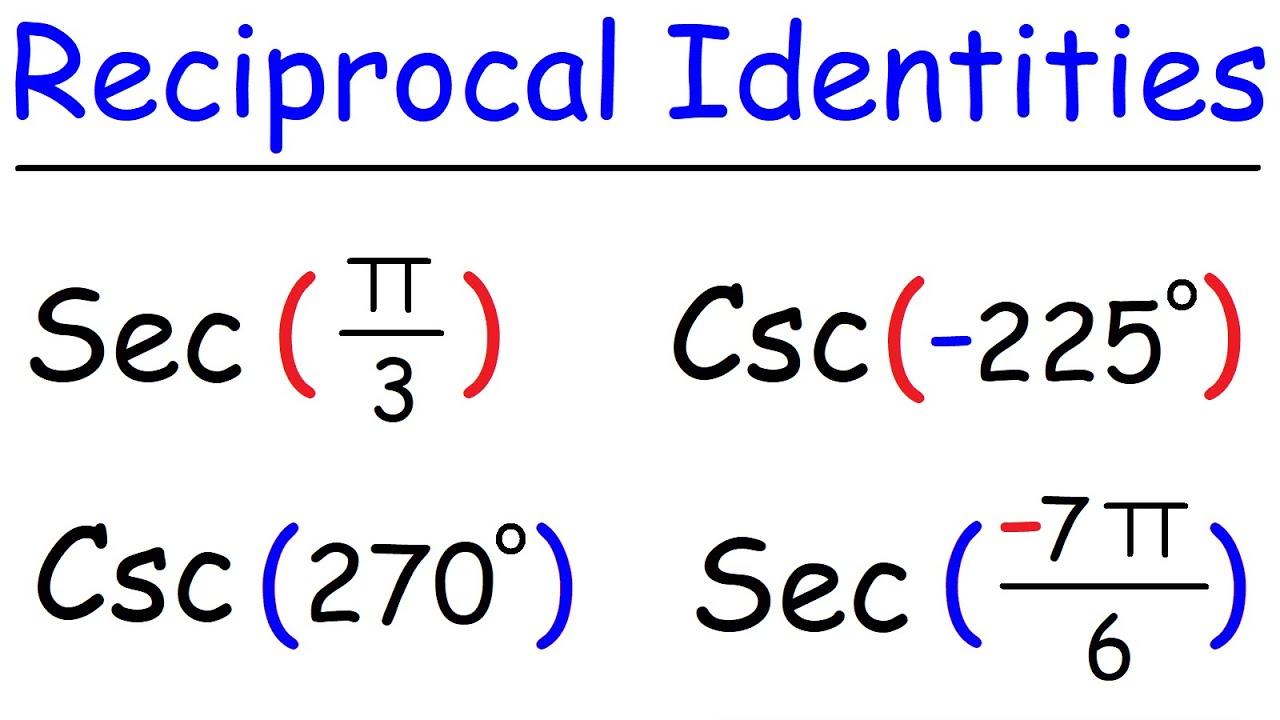
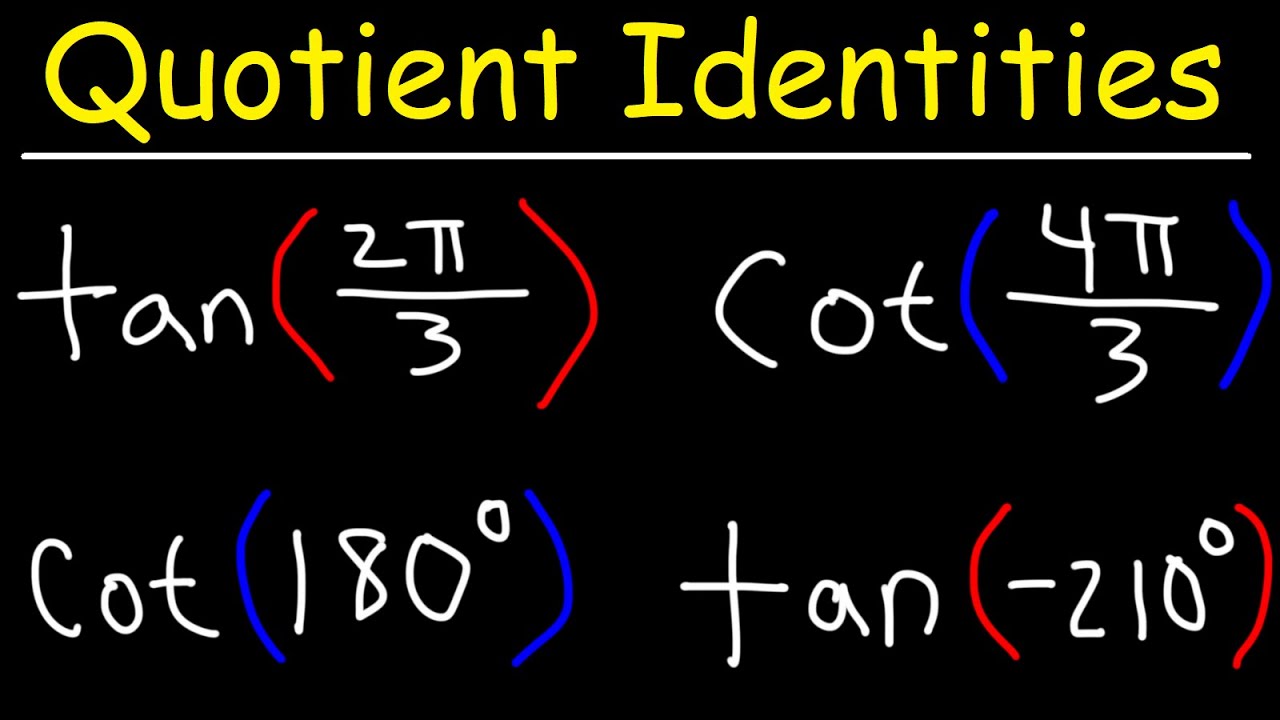
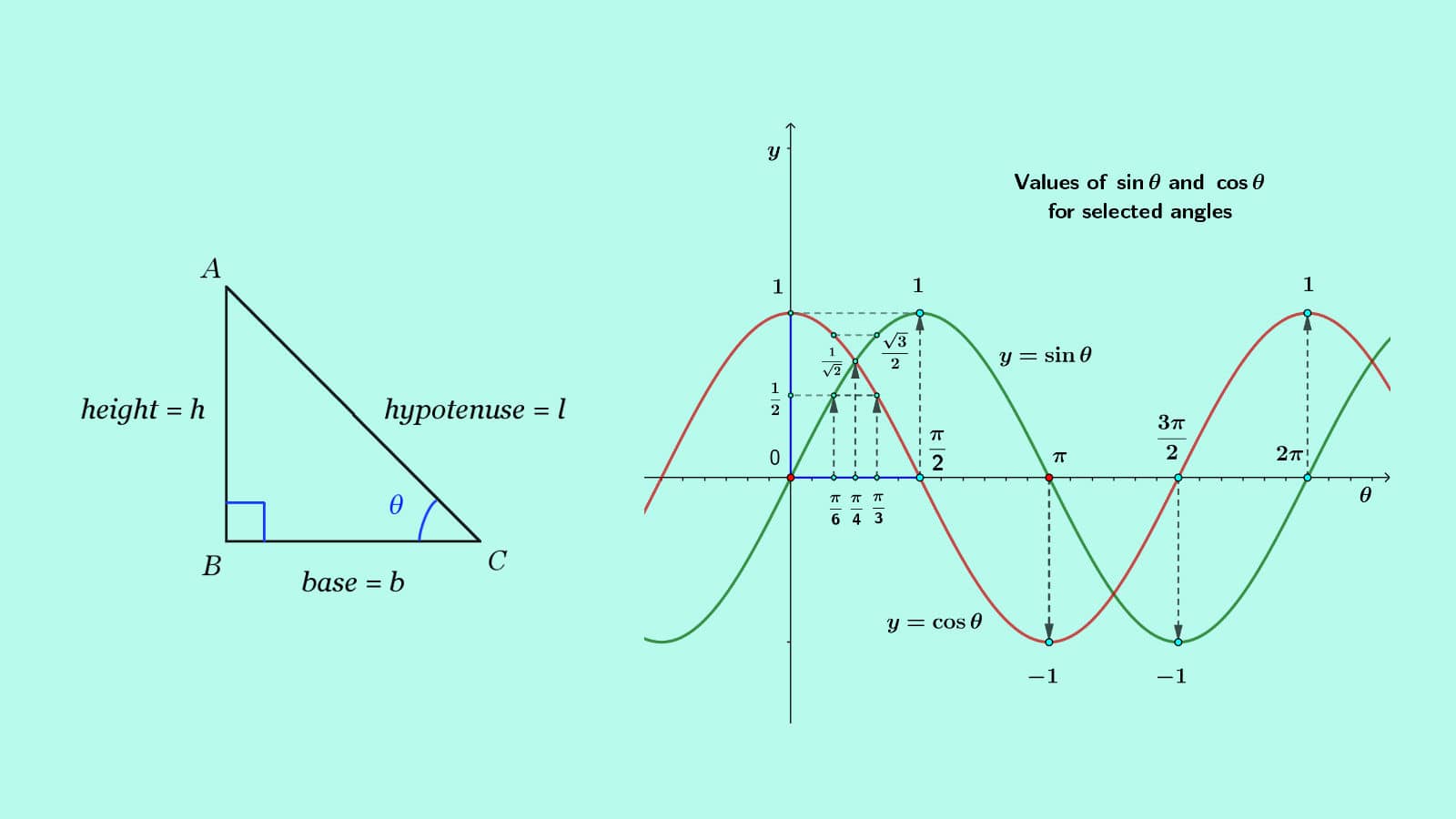
Introduction Trigonometric identities are fundamental tools in mathematics that establish relationships between various trigonometric functions. Understanding and applying these identities is crucial in solving complex problems in calculus, geometry, physics, and engineering. In this comprehensive guide, we'll delve into the essential trigonometric identities and explore their wide-ranging applications. Basic Trigonometric Functions Before delving into identities, it's important to familiarize oneself with the basic trigonometric functions: Sine ( � � � sin): � � � � � � � � ℎ � � � � � � � � � hypotenuse opposite Cosine ( � � � cos): � � � � � � � � ℎ � � � � � � � � � hypotenuse adjacent Tangent ( � � � tan): � � � � � � � � � � � � � � � � adjacent opposite Cosecant ( � � � csc): ℎ � � � � � � � � � � � � � � � � � opposite hypotenuse Secant ( � � � sec): ℎ � � � � � � � � � � � � � � � � � adjacent hypotenuse Cotangent ( � � � cot): � � � � � � � � � � � � � � � � opposite adjacent These functions form the basis for all trigonometric identities. Pythagorean Identities The Pythagorean identities are perhaps the most well-known and fundamental trigonometric relationships: � � � 2 ( � ) + � � � 2 ( � ) = 1 sin 2 (x)+cos 2 (x)=1 1 + � � � 2 ( � ) = � � � 2 ( � ) 1+tan 2 (x)=sec 2 (x) 1 + � � � 2 ( � ) = � � � 2 ( � ) 1+cot 2 (x)=csc 2 (x) These identities establish the relationships between the trigonometric functions of a given angle in a right triangle. Reciprocal Identities Reciprocal identities express each trigonometric function in terms of its reciprocal: � � � ( � ) = 1 � � � ( � ) sin(x)= csc(x) 1 � � � ( � ) = 1 � � � ( � ) cos(x)= sec(x) 1 � � � ( � ) = 1 � � � ( � ) tan(x)= cot(x) 1 � � � ( � ) = 1 � � � ( � ) csc(x)= sin(x) 1 � � � ( � ) = 1 � � � ( � ) sec(x)= cos(x) 1 � � � ( � ) = 1 � � � ( � ) cot(x)= tan(x) 1 These identities are crucial for simplifying complex expressions. Quotient Identities The quotient identities express tangent, cotangent, secant, and cosecant in terms of sine and cosine: � � � ( � ) = � � � ( � ) � � � ( � ) tan(x)= cos(x) sin(x) � � � ( � ) = � � � ( � ) � � � ( � ) cot(x)= sin(x) cos(x) � � � ( � ) = 1 � � � ( � ) sec(x)= cos(x) 1 � � � ( � ) = 1 � � � ( � ) csc(x)= sin(x) 1 These identities are particularly useful when dealing with trigonometric functions in terms of a single variable. Co-function Identities Co-function identities express the complement of an angle's trigonometric function in terms of the original function: � � � ( � 2 − � ) = � � � ( � ) sin( 2 π −x)=cos(x) � � � ( � 2 − � ) = � � � ( � ) cos( 2 π −x)=sin(x) � � � ( � 2 − � ) = 1 � � � ( � ) tan( 2 π −x)= tan(x) 1 � � � ( � 2 − � ) = � � � ( � ) csc( 2 π −x)=sec(x) � � � ( � 2 − � ) = � � � ( � ) sec( 2 π −x)=csc(x) � � � ( � 2 − � ) = 1 � � � ( � ) cot( 2 π −x)= cot(x) 1 These identities relate the trigonometric functions of an angle and its complement. Double Angle Identities Double angle identities express the trigonometric functions of 2 � 2x in terms of � x: � � � ( 2 � ) = 2 � � � ( � ) � � � ( � ) sin(2x)=2sin(x)cos(x) � � � ( 2 � ) = � � � 2 ( � ) − � � � 2 ( � ) = 2 � � � 2 ( � ) − 1 = 1 − 2 � � � 2 ( � ) cos(2x)=cos 2 (x)−sin 2 (x)=2cos 2 (x)−1=1−2sin 2 (x) � � � ( 2 � ) = 2 � � � ( � ) 1 − � � � 2 ( � ) tan(2x)= 1−tan 2 (x) 2tan(x) These identities are invaluable for simplifying expressions involving double angles. Applications in Calculus and Geometry Trigonometric identities play a pivotal role in calculus, where they are used to integrate and differentiate trigonometric functions. They are also essential in solving problems involving angles, triangles, and circles in geometry. Applications in Physics and Engineering
In physics, trigonometric identities are used extensively in the analysis of periodic phenomena, oscillations, waves, and harmonic motion. In engineering, they find applications in fields such as signal processing, control systems, and electrical circuits. Conclusion Mastering trigonometric identities is a crucial step in becoming proficient in advanced mathematics, physics, and engineering. These identities serve as powerful tools for solving complex problems, simplifying expressions, and understanding the relationships between various trigonometric functions. By incorporating these identities into your mathematical toolkit, you'll be better equipped to tackle a wide range of mathematical challenges in both academic and practical settings.
0 Comments
Leave a Reply. |
Categories
Categories
All
|






 RSS Feed
RSS Feed