|
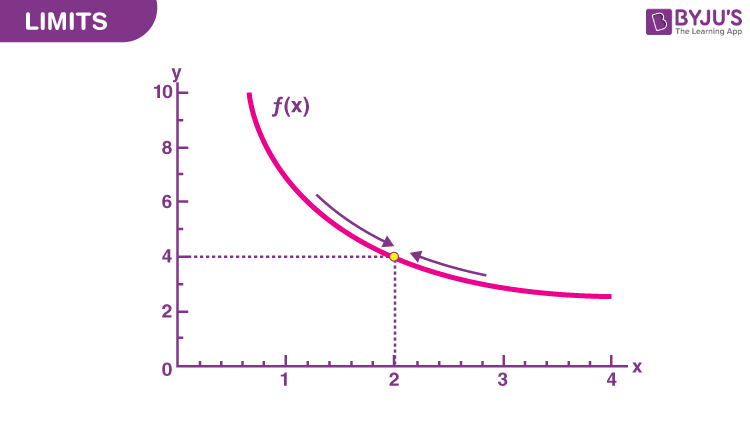
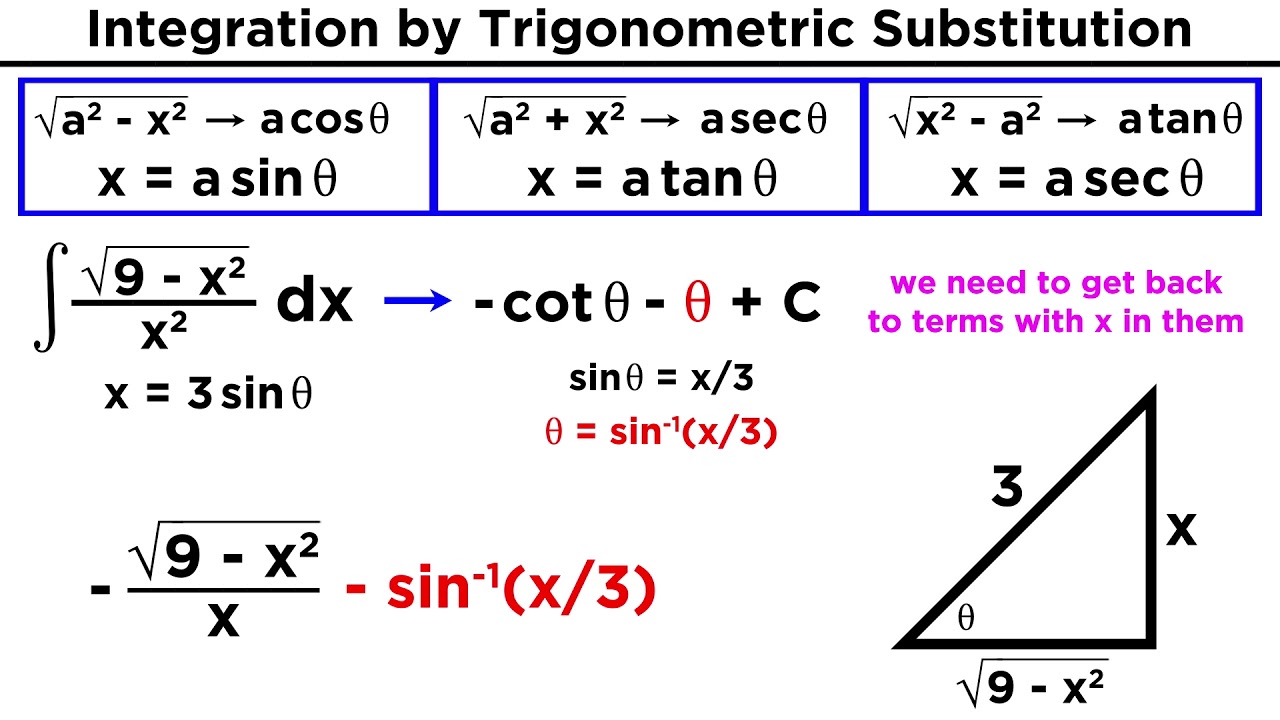
Introduction Advanced Calculus is a powerful branch of mathematics that delves into concepts like limits, continuity, differentiation, and integration in greater depth than introductory calculus courses. It serves as a foundation for various fields including physics, engineering, economics, and computer science. In this article, we will explore essential formulas and techniques to help you master Advanced Calculus. Limits and Continuity Definition of a Limit: The limit of a function � ( � ) f(x) as � x approaches � c is denoted by lim � → � � ( � ) lim x→c f(x) and represents the value � L that � ( � ) f(x) approaches as � x gets arbitrarily close to � c. Continuity: A function � ( � ) f(x) is continuous at � = � x=c if lim � → � � ( � ) = � ( � ) lim x→c f(x)=f(c), meaning the function does not have any holes, jumps, or asymptotes at � = � x=c. Differentiation Techniques Power Rule: � � � ( � � ) = � � � − 1 dx d (x n )=nx n−1 Chain Rule: � � � [ � ( � ( � ) ) ] = � ′ ( � ( � ) ) ⋅ � ′ ( � ) dx d [f(g(x))]=f ′ (g(x))⋅g ′ (x) Product Rule: � � � ( � ⋅ � ) = � ′ � + � � ′ dx d (u⋅v)=u ′ v+uv ′ Quotient Rule: � � � ( � � ) = � ′ � − � � ′ � 2 dx d ( v u )= v 2 u ′ v−uv ′ Implicit Differentiation: Useful for finding derivatives of implicitly defined functions. Trigonometric Functions: Memorize the derivatives of sine, cosine, tangent, and their inverses. Integration Techniques Basic Integration Rules: ∫ � � � � = � � + 1 � + 1 + � ∫x n dx= n+1 x n+1 +C, where � ≠ − 1 n =−1. ∫ � � � � = � � + � ∫e x dx=e x +C. ∫ sin ( � ) � � = − cos ( � ) + � ∫sin(x)dx=−cos(x)+C. ∫ cos ( � ) � � = sin ( � ) + � ∫cos(x)dx=sin(x)+C. Integration by Parts: ∫ � � � = � � − ∫ � � � ∫udv=uv−∫vdu, where � u and � v are continuously differentiable functions. Trigonometric Substitution: Useful for integrals involving radical expressions, completing the square, and inverse trigonometric functions. Partial Fractions Decomposition: Used to break down rational functions into simpler fractions for easier integration. Integration by Substitution: Involves substituting variables to simplify the integral. Sequences and Series Convergence and Divergence: Understand the criteria for convergence (e.g., geometric series, p-series) and divergence (e.g., harmonic series). Tests for Convergence: Know and apply tests such as the Comparison Test, Ratio Test, and Integral Test. Taylor and Maclaurin Series: Learn how to find Taylor and Maclaurin series expansions of functions around a given point. Multivariable Calculus Partial Derivatives: Extend differentiation to functions of multiple variables. Gradient and Directional Derivative: Understand the concept of a vector representing the rate of change of a function. Double and Triple Integrals: Apply integration techniques to functions of two or three variables. Line Integrals and Surface Integrals: Calculate integrals over curves and surfaces in space. Vector Calculus Vector Functions and Parametric Equations: Representing curves and surfaces using vectors. Dot Product and Cross Product: Understand and apply these operations to vectors. Vector Fields and Line Integrals: Study how vector fields behave over curves. Green's Theorem, Stokes' Theorem, and Divergence Theorem: Fundamental theorems relating line and surface integrals. Conclusion Mastering Advanced Calculus involves a deep understanding of concepts such as limits, continuity, differentiation, and integration. It's important to not only memorize formulas but also to understand the underlying principles and techniques. With a solid grasp of these essential concepts and techniques, you'll be well-equipped to tackle complex problems and apply Advanced Calculus in various fields of study and research. Remember, practice and persistence are key to becoming proficient in this challenging yet rewarding branch of mathematics.
0 Comments
Leave a Reply. |
Categories
Categories
All
|



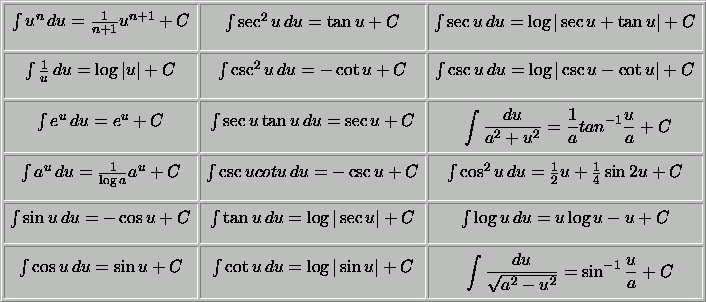
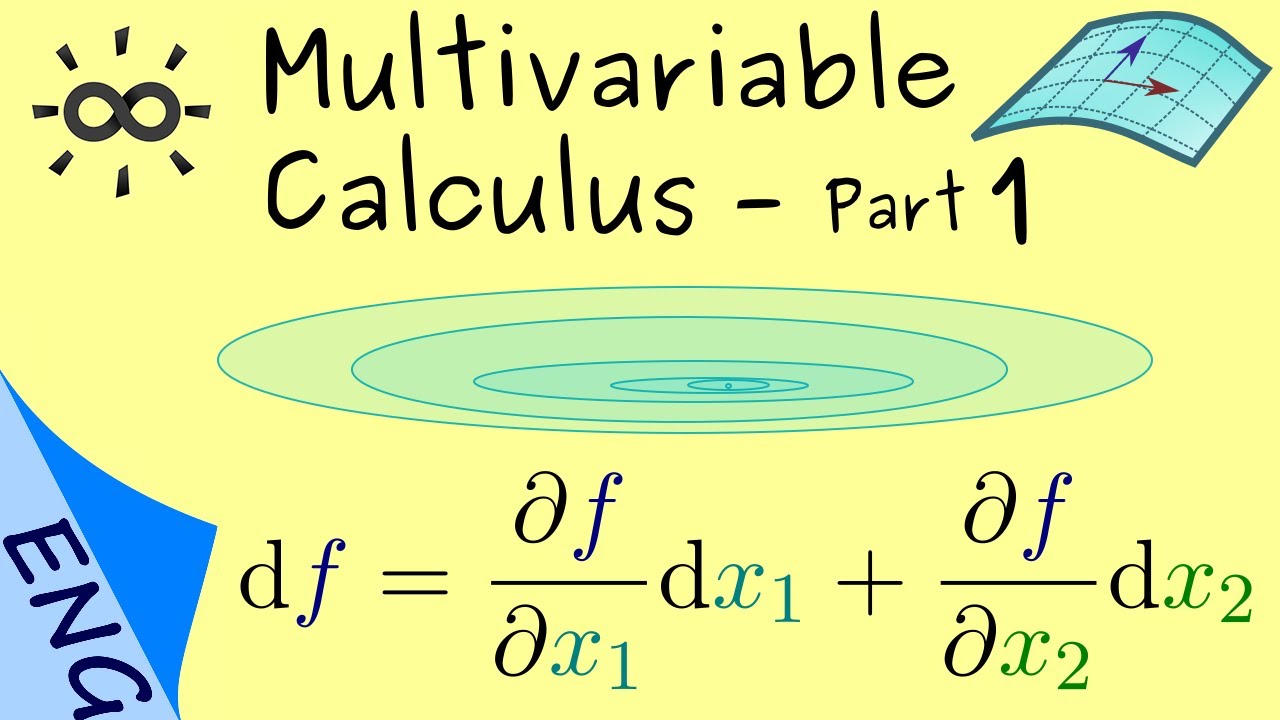



 RSS Feed
RSS Feed