|
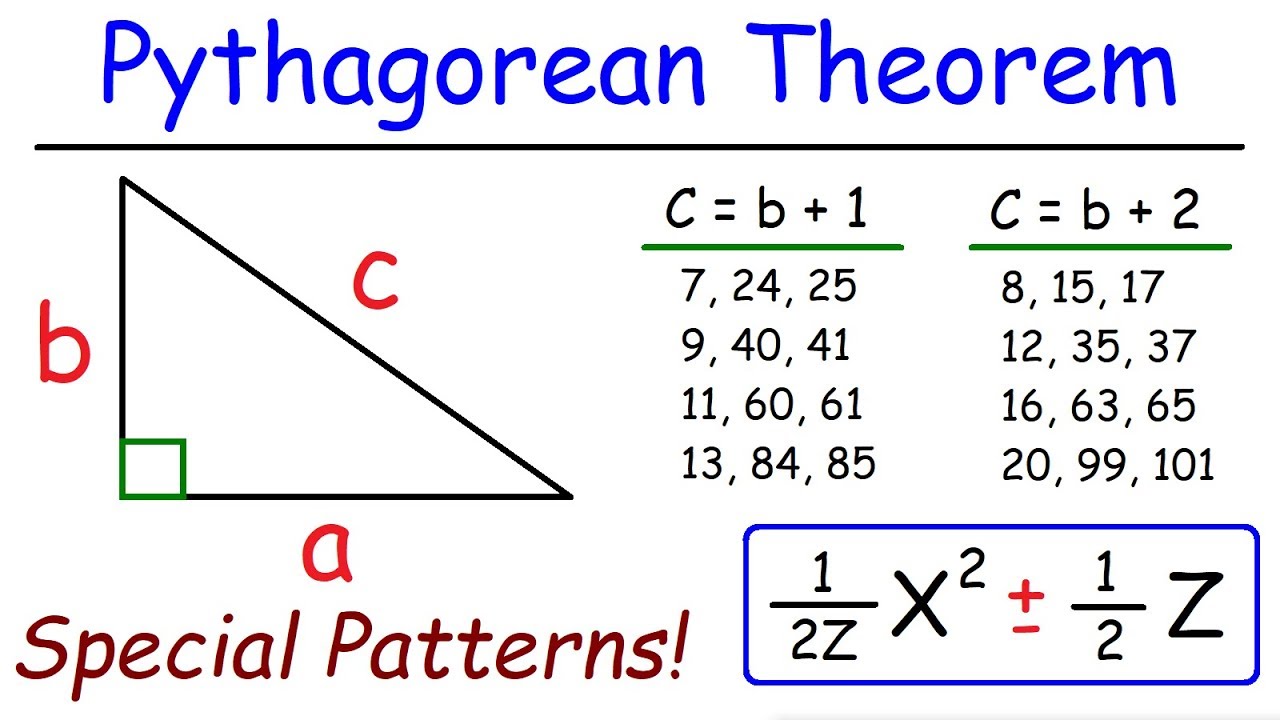
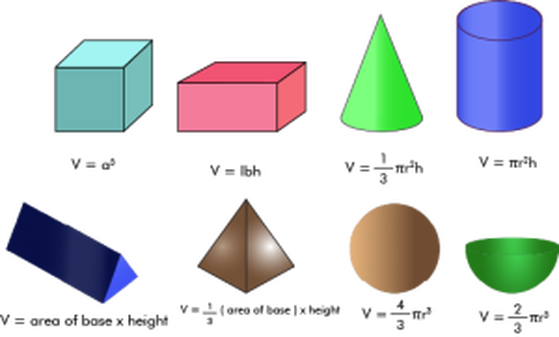
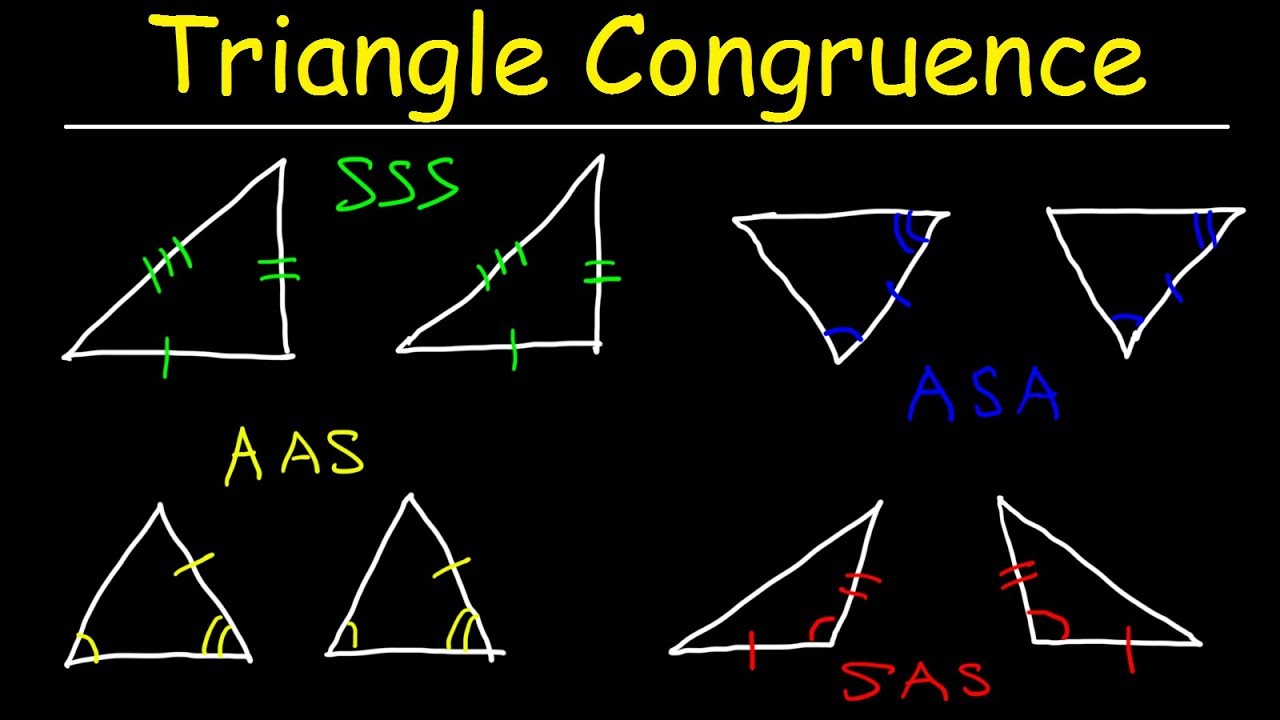
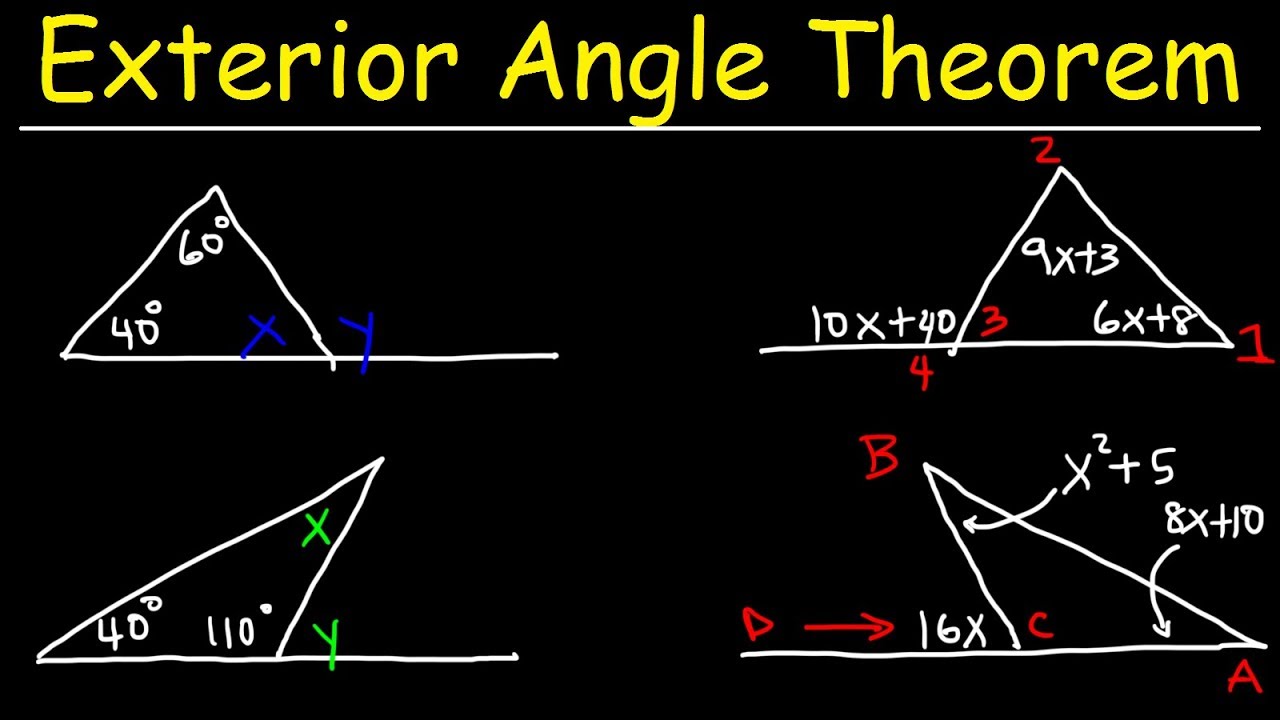
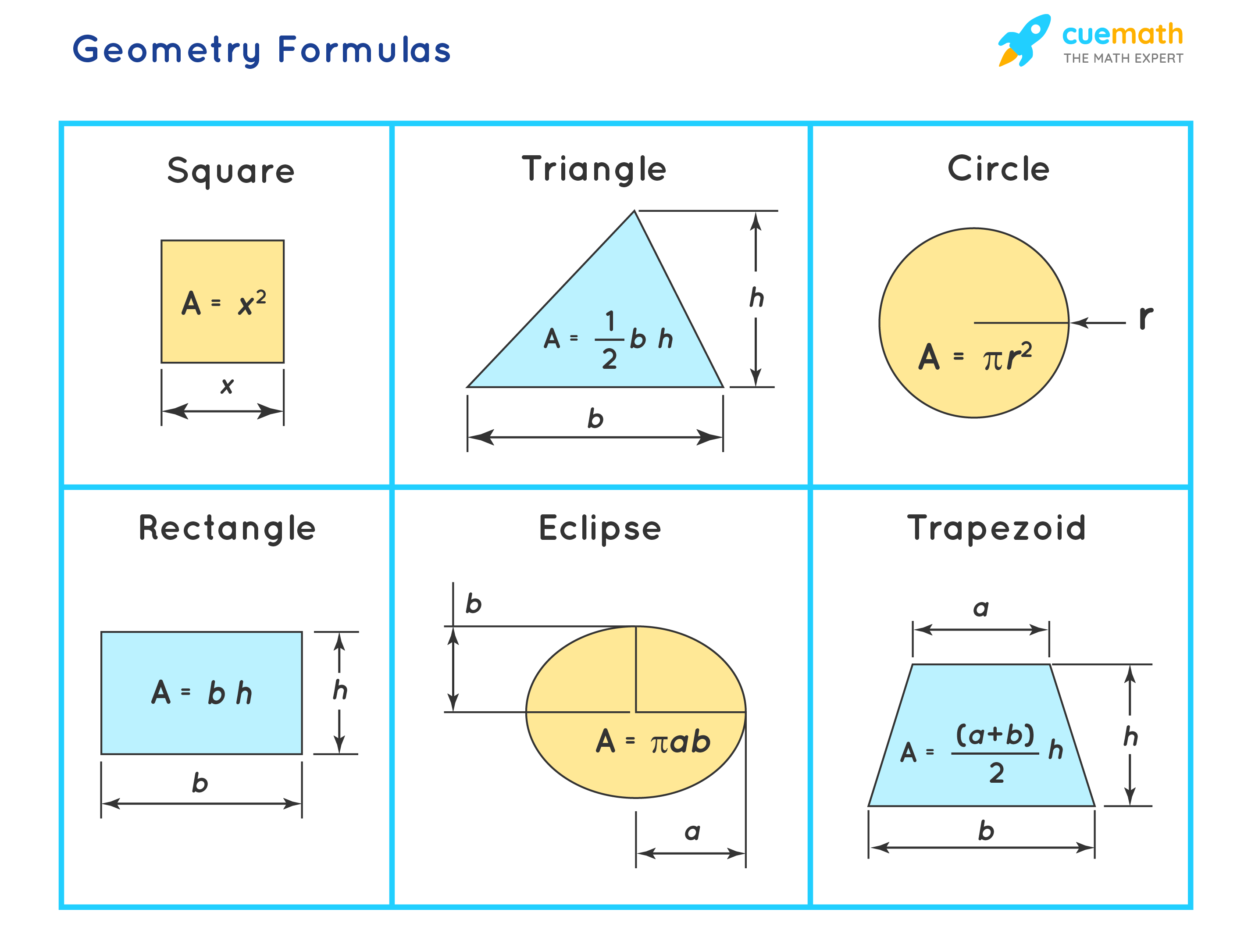
Introduction Geometry is a branch of mathematics that deals with the properties and relationships of shapes, sizes, and angles. It is a fundamental field of study with applications in various fields including engineering, architecture, physics, and more. To excel in geometry, it is crucial to understand and apply key theorems and formulas. In this article, we will explore the fundamental theorems and formulas that are essential for success in geometry. Pythagorean Theorem The Pythagorean Theorem is one of the most well-known and fundamental theorems in geometry. It states that in a right-angled triangle, the square of the length of the hypotenuse ( � c) is equal to the sum of the squares of the lengths of the other two sides ( � a and � b). � 2 = � 2 + � 2 c 2 =a 2 +b 2 This theorem is invaluable in solving problems involving right triangles and is the basis for many other geometric concepts. Area Formulas Understanding the formulas for calculating the area of common shapes is crucial in geometry. Here are some key area formulas: Rectangle: Area ( � A) = Length ( � l) × Width ( � w) Triangle: Area ( � A) = 1 2 2 1 × Base ( � b) × Height ( ℎ h) Circle: Area ( � A) = � � 2 πr 2 (where � r is the radius) Trapezoid: Area ( � A) = 1 2 2 1 × Sum of bases ( � 1 + � 2 b 1 +b 2 ) × Height ( ℎ h) Knowing these formulas enables you to find the area of various shapes, which is essential in both geometry and real-world applications. Volume Formulas Volume formulas are used to calculate the space occupied by three-dimensional objects. Here are some important volume formulas: Cube: Volume ( � V) = � 3 s 3 (where � s is the length of a side) Cylinder: Volume ( � V) = � � 2 ℎ πr 2 h (where � r is the radius and ℎ h is the height) Sphere: Volume ( � V) = 4 3 � � 3 3 4 πr 3 (where � r is the radius) Cone: Volume ( � V) = 1 3 � � 2 ℎ 3 1 πr 2 h (where � r is the radius and ℎ h is the height) These formulas are essential for calculating volumes in a wide range of contexts. Similar Triangles Similar triangles have the same shape but possibly different sizes. Two triangles are similar if their corresponding angles are equal and their corresponding sides are in proportion. This fundamental concept is used in a variety of geometric problems, especially those involving indirect measurements. Congruence Theorems Congruent figures have the same shape and size. There are several congruence theorems that establish when two figures are congruent: Side-Angle-Side (SAS): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent. Side-Side-Side (SSS): If the three sides of one triangle are congruent to the three sides of another triangle, the triangles are congruent. Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, the triangles are congruent. These theorems are essential in proving the congruence of triangles, which is a foundational concept in geometry. Angle Sum and Exterior Angle Theorems Angle Sum Theorem: In any triangle, the sum of the measures of the three interior angles is always 18 0 ∘ 180 ∘ . Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles. These theorems are used extensively in triangle geometry and are crucial for understanding the relationships between angles in polygons. Conclusion Mastering the key theorems and formulas in geometry is essential for success in this branch of mathematics. Understanding concepts like the Pythagorean Theorem, area and volume formulas, congruence theorems, and similar triangles lays a strong foundation for solving complex geometric problems. Whether you're a student studying geometry in school or a professional using it in your field, these fundamentals are invaluable. By applying these theorems and formulas, you'll be well-equipped to tackle a wide range of geometric challenges with confidence and proficiency.
0 Comments
Leave a Reply. |
Categories
Categories
All
|





 RSS Feed
RSS Feed