|
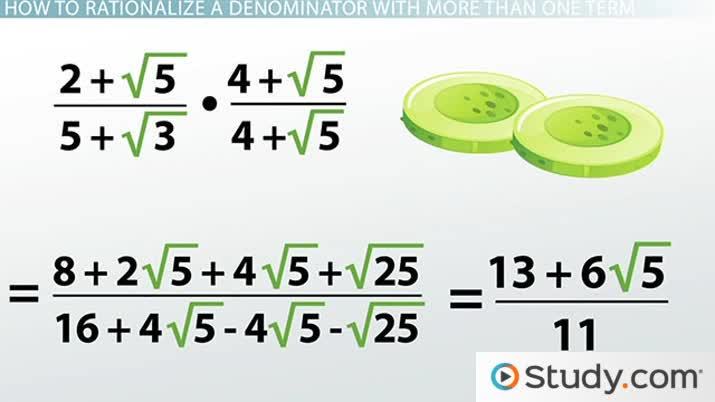
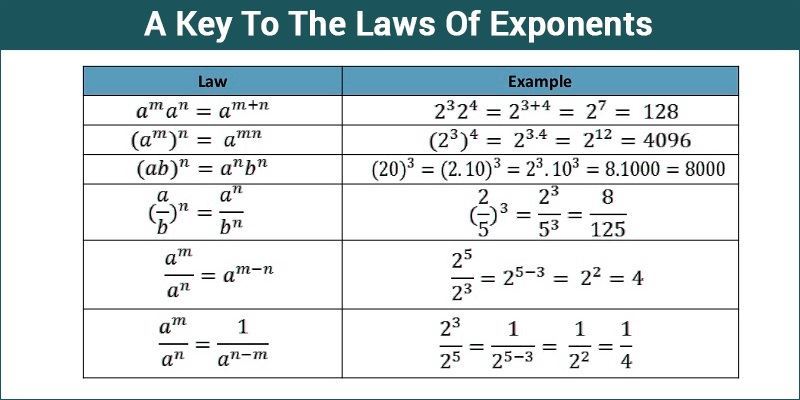
Introduction Algebraic manipulations form the foundation of solving equations and understanding complex mathematical expressions. Whether you're a student grappling with algebra or a professional navigating intricate equations, mastering these techniques is essential. In this article, we'll explore various tips and tricks to help you simplify equations and tackle algebraic challenges with confidence. Combining Like Terms One of the most basic but crucial techniques in algebra is combining like terms. This involves adding or subtracting terms with the same variables and exponents. Example: Given the expression 3 � + 2 � − � − 5 � 3x+2y−x−5y, combine like terms to get 2 � − 3 � 2x−3y. Distributive Property The distributive property allows you to multiply a term or expression by every term inside parentheses. This is especially useful for factoring and expanding expressions. Example: 3 ( � + 2 ) = 3 � + 6 3(x+2)=3x+6 Factoring Factoring involves rewriting an expression as a product of simpler expressions. This is a powerful tool for simplification and solving equations. Example: Factor � 2 − 4 x 2 −4 to get ( � + 2 ) ( � − 2 ) (x+2)(x−2). Expanding and FOIL The FOIL method (First, Outer, Inner, Last) is a technique for multiplying two binomials. It's crucial in simplifying expressions involving quadratic terms. Example: ( � + 2 ) ( � − 3 ) = � 2 − � − 6 (x+2)(x−3)=x 2 −x−6 Solving for a Variable If you have an equation with multiple variables, isolating one variable in terms of the others can simplify the problem. Example: Solve for � y in the equation 3 � − 2 � = 8 3x−2y=8 to get � = 3 2 � − 4 y= 2 3 x−4. Common Denominator When adding or subtracting fractions, finding a common denominator allows you to combine them into a single fraction. Example: 1 3 + 2 5 = 5 15 + 6 15 = 11 15 3 1 + 5 2 = 15 5 + 15 6 = 15 11 . Rationalizing Denominators Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. This is essential for simplifying expressions involving square roots. Example: Rationalize the denominator of 1 3 3 1 to get 3 3 3 3 . Completing the Square Completing the square is a technique used to rewrite quadratic expressions into a perfect square trinomial. Example: Complete the square for � 2 − 6 � x 2 −6x to get ( � − 3 ) 2 − 9 (x−3) 2 −9. Substitution Substitution involves replacing variables with known values or expressions to simplify complex equations. Example: Substitute � = � + 2 u=x+2 in the equation � 2 − 4 � + 4 = 0 u 2 −4u+4=0 to get � − 2 = 0 u−2=0, which leads to � = − 2 x=−2. Canceling Terms In fractions, you can often cancel out common factors between the numerator and denominator to simplify the expression. Example: 3 � 6 = � 2 6 3x = 2 x . Using Exponent Rules Understanding exponent rules is crucial for simplifying expressions with exponents. Example: � � ⋅ � � = � � + � x a ⋅x b =x a+b . Identifying Special Cases Recognizing special cases, like perfect squares or the difference of squares, can lead to immediate simplifications. Example: � 2 − 25 = ( � + 5 ) ( � − 5 ) x 2 −25=(x+5)(x−5). Conclusion Algebraic manipulations are indispensable tools in mathematics, providing the means to simplify expressions and solve equations. By mastering these techniques, you'll gain the confidence to tackle a wide range of algebraic challenges. Remember, practice is key to becoming proficient, so apply these tips to various problems and seek additional resources or guidance when needed. With dedication and a systematic approach, you'll be well-equipped to excel in algebra and beyond.
0 Comments
Leave a Reply. |
Categories
Categories
All
|














 RSS Feed
RSS Feed